振動と振動計
振動について
振動の大きさの表現や測定量(加速度・速度・変位)など、振動測定のために必要な基礎知識について解説します。
振動とは?
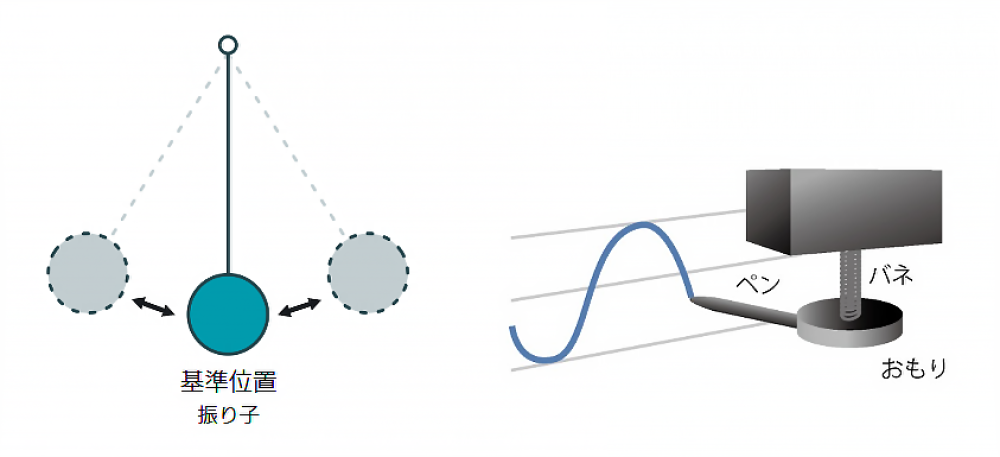
振動とは、ある基準位置を中心に物体が行ったり来たりして、繰り返し動く現象です。
一般的な振動は、いろいろな種類の単振動が複雑に組み合わされた波形として表現できます。

振動の大きさの表現
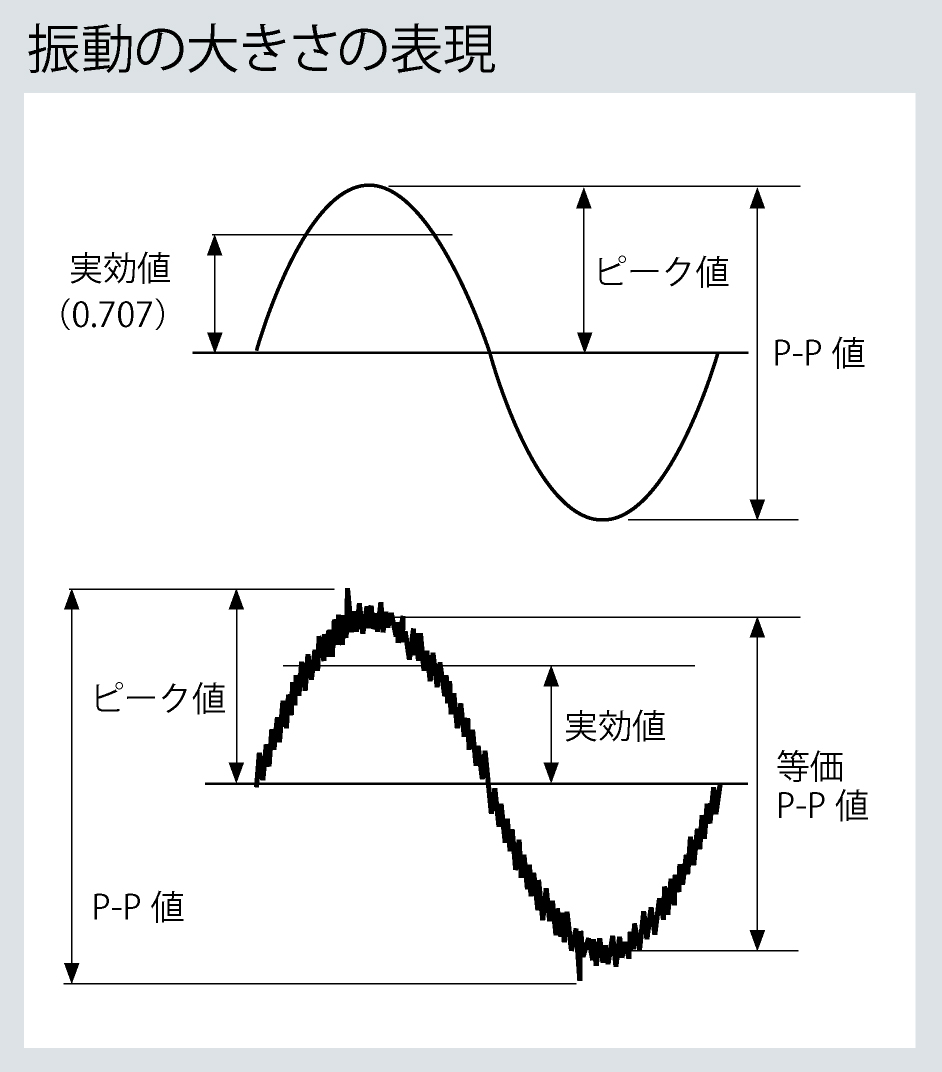
振動は、横軸を「時間」、縦軸を「振動の大きさ」、中央の線を0の基準として±の波形で表すことができます。
振動の大きさを表す値として、以下の値があります。
【ピーク値】・・・・・・・・・・・・ 片側振幅の最大値
【実効値】・・・・・・・・・・・・・ 瞬時値の2乗平均の平方根
【ピーク to ピーク値(P-P値)】・・・極大と極小値の差の最大
【等価ピーク値(EQピーク値)】・・・実効値の√2倍
【等価P-P値】・・・・・・・・・・・・等価ピーク値の2倍の値
【波高率(クレストファクタ)】・・・・ピーク値/実効値
加速度、速度、変位とは
振動を表す基本的な物理量には、「加速度、速度、変位」があります。 それぞれの物理量には特長があり、測定の目的により使い分けて計測することにより、機械の状態を適切に把握することができます。

変位とは(単位:μm、mm など)
基準位置からの移動距離を表す量です。
例として、自動車が100 m移動した場合、移動距離「100 m」が変位になります。
振動では物体が静止位置から移動した距離を表し正負に変化します。

速度とは(単位:mm/s、m/s など)
単位時間当たりの変動を表す量です。振動エネルギに関係します。
例として、自動車が10秒間で100 m移動した場合、移動距離(100 m)を時間(10秒)で割った値「10 m/s」が速度となります。
振動では、短時間の内に変位の大きさや方向が変化するため、速度も一定ではなく変化します。
速度=変位×2π×振動数の関係があります。
加速度とは(単位:m/s²、mm/s² など)
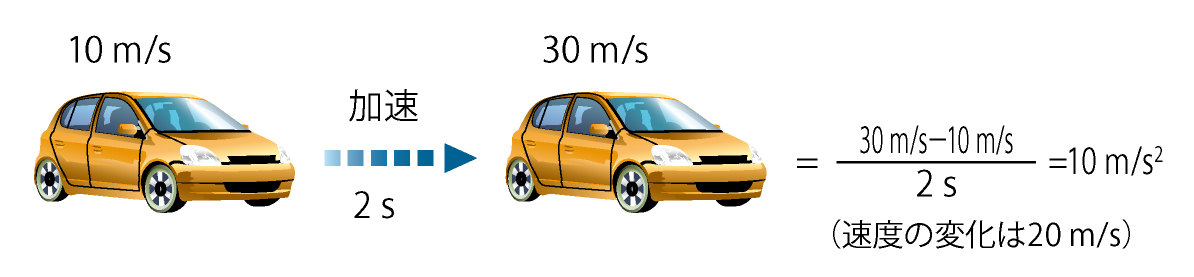
単位時間当たりの速度の変化を表す量です。衝撃力のような力の大きさに比例します。
例として、10 m/sで移動している自動車が2秒間で30 m/sに加速した場合、速度の変化量(20 m/s)を時間(2秒)で割った値
「10 m/s²」が加速度となります。
「10 m/s²」が加速度となります。
振動では、短時間の内に速度の大きさや方向が変化するため、加速度も一定ではなく変化します。
加速度=速度×2π×振動数の関係があります。
加速度、速度、変位の使用方法
|
変位 |
・低域振動数の測定(200 Hz以下) ・変化量そのものが問題になる場合 ・引っ張りや圧縮などによる静的な変形による損傷問題 ・接触の危機、加工精度 |
|---|---|
|
速度 |
・中域振動数の測定(10 Hz~1 kHz) ・アンバランス、ミスアライメント、ボルトの緩み、ガタなどの検出 ・振動シビアリティ(ISO 10816、JIS B 0906) ・金属疲労度 |
|
加速度 |
・高域振動数の測定(1 kHz以上) ・軸受や歯車などの欠陥検出 |
目次




